Введение в алгоритм сортировки слиянием
Сортировка слиянием – это алгоритм сортировки, основанный на технике «разделяй и властвуй». Это один из самых эффективных алгоритмов сортировки.
В этой статье вы узнаете о работе алгоритма сортировки слиянием, алгоритме сортировки слиянием, его временной и пространственной сложности и его реализации на различных языках программирования, таких как C ++, Python и JavaScript.
Как работает алгоритм сортировки слиянием?
Сортировка слиянием работает по принципу «разделяй и властвуй». Сортировка слиянием многократно разбивает массив на два равных подмассива, пока каждый подмассив не будет состоять из одного элемента. Наконец, все эти подмассивы объединяются, так что результирующий массив сортируется.
Более эффективно эту концепцию можно пояснить на примере. Рассмотрим несортированный массив со следующими элементами: {16, 12, 15, 13, 19, 17, 11, 18}.
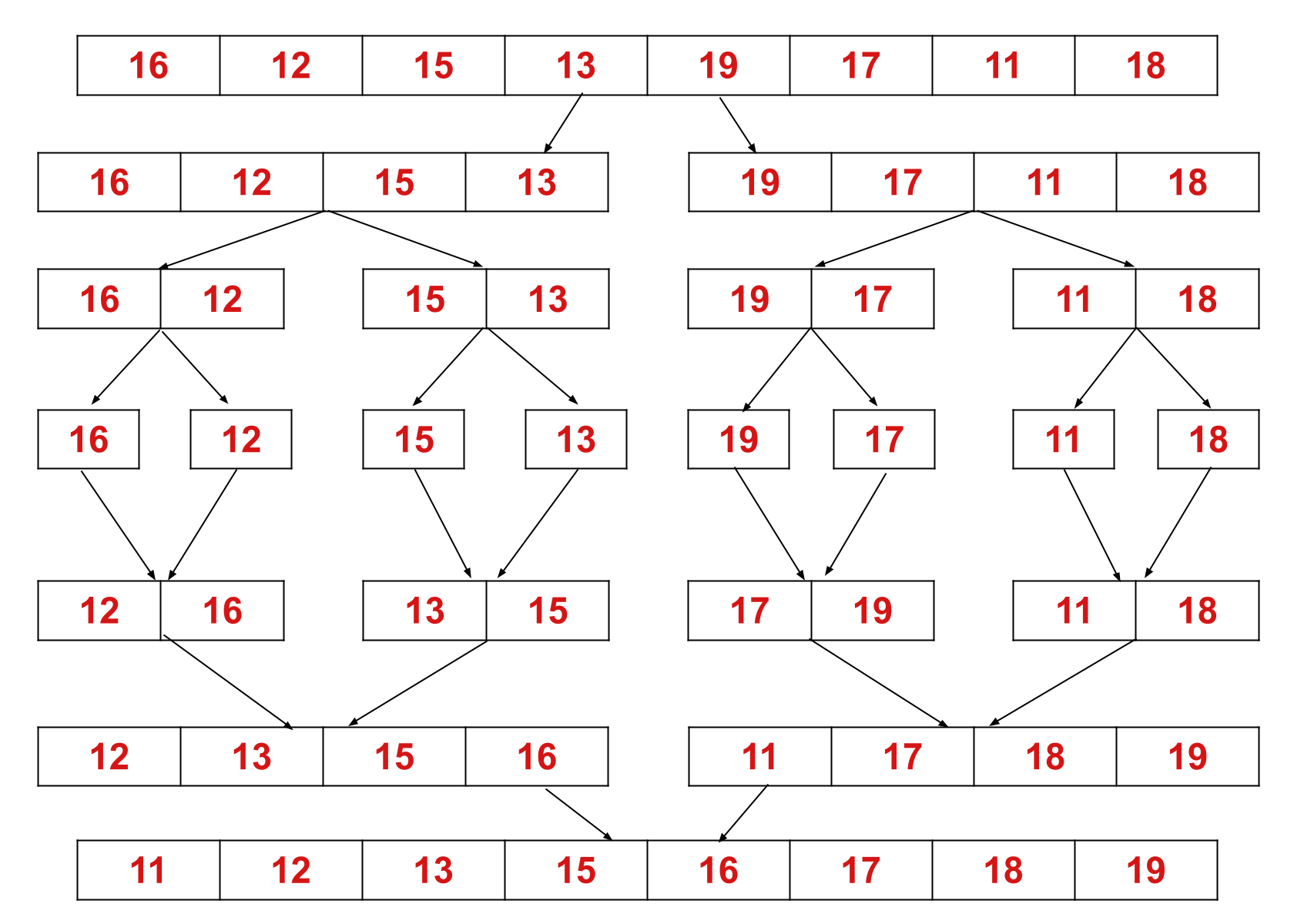
Здесь алгоритм сортировки слиянием делит массив на две половины, вызывает себя для двух половин, а затем объединяет две отсортированные половины.
Алгоритм сортировки слиянием
Ниже представлен алгоритм сортировки слиянием:
MergeSort(arr[], leftIndex, rightIndex)
if leftIndex >= rightIndex
return
else
Find the middle index that divides the array into two halves:
middleIndex = leftIndex + (rightIndex-leftIndex)/2
Call mergeSort() for the first half:
Call mergeSort(arr, leftIndex, middleIndex)
Call mergeSort() for the second half:
Call mergeSort(arr, middleIndex+1, rightIndex)
Merge the two halves sorted in step 2 and 3:
Call merge(arr, leftIndex, middleIndex, rightIndex)
Временная и пространственная сложность алгоритма сортировки слиянием
Алгоритм сортировки слиянием можно выразить в виде следующего рекуррентного соотношения:
Т (п) = 2Т (п / 2) + О (п)
После решения этого рекуррентного отношения с помощью теоремы мастера или метода повторяющегося дерева вы получите решение как O (n logn). Таким образом, временная сложность алгоритма сортировки слиянием составляет O (n logn) .
Оптимальная временная сложность сортировки слиянием: O (n logn)
Средняя временная сложность сортировки слиянием: O (n logn)
Наихудшая временная сложность сортировки слиянием: O (n logn)
Сложность вспомогательного пространства алгоритма сортировки слиянием составляет O (n), поскольку n вспомогательного пространства требуется в реализации сортировки слиянием.
Реализация алгоритма сортировки слиянием в C ++
Ниже представлена реализация алгоритма сортировки слиянием на C ++:
// C++ implementation of the
// merge sort algorithm
#include <iostream>
using namespace std;
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
void merge(int arr[], int leftIndex, int middleIndex, int rightIndex)
{
int leftSubarraySize = middleIndex - leftIndex + 1;
int rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
int L[leftSubarraySize], R[rightSubarraySize];
// Copying data to temporary arrays L[] and R[]
for (int i = 0; i < leftSubarraySize; i++)
L[i] = arr[leftIndex + i];
for (int j = 0; j < rightSubarraySize; j++)
R[j] = arr[middleIndex + 1 + j];
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
int i = 0;
// Initial index of Right subarray
int j = 0;
// Initial index of merged subarray
int k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int leftIndex, int rightIndex)
{
if(leftIndex >= rightIndex)
{
return;
}
int middleIndex = leftIndex + (rightIndex - leftIndex)/2;
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 16, 12, 15, 13, 19, 17, 11, 18 };
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Unsorted array:" << endl;
printArray(arr, size);
mergeSort(arr, 0, size - 1);
cout << "Sorted array:" << endl;
printArray(arr, size);
return 0;
}Выход:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19Реализация алгоритма сортировки слиянием в JavaScript
Ниже представлена реализация алгоритма сортировки слиянием в JavaScript:
// JavaScript implementation of the
// merge sort algorithm
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
function merge(arr, leftIndex, middleIndex, rightIndex) {
let leftSubarraySize = middleIndex - leftIndex + 1;
let rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
var L = new Array(leftSubarraySize);
var R = new Array(rightSubarraySize);
// Copying data to temporary arrays L[] and R[]
for(let i = 0; i<leftSubarraySize; i++) {
L[i] = arr[leftIndex + i];
}
for (let j = 0; j<rightSubarraySize; j++) {
R[j] = arr[middleIndex + 1 + j];
}
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
var i = 0;
// Initial index of Right subarray
var j = 0;
// Initial index of merged subarray
var k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
function mergeSort(arr, leftIndex, rightIndex) {
if(leftIndex >= rightIndex) {
return
}
var middleIndex = leftIndex + parseInt((rightIndex - leftIndex)/2);
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
function printArray(arr, size) {
for(let i = 0; i<size; i++) {
document.write(arr[i] + " ");
}
document.write("<br>");
}
// Driver code:
var arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ];
var size = arr.length;
document.write("Unsorted array:<br>");
printArray(arr, size);
mergeSort(arr, 0, size - 1);
document.write("Sorted array:<br>");
printArray(arr, size);Выход:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19
Реализация алгоритма сортировки слиянием на Python
Ниже представлена реализация алгоритма сортировки слиянием в Python:
# Python implementation of the
# merge sort algorithm
def mergeSort(arr):
if len(arr) > 1:
# Finding the middle index of the array
middleIndex = len(arr)//2
# Left half of the array
L = arr[:middleIndex]
# Right half of the array
R = arr[middleIndex:]
# Sorting the first half of the array
mergeSort(L)
# Sorting the second half of the array
mergeSort(R)
# Initial index of Left subarray
i = 0
# Initial index of Right subarray
j = 0
# Initial index of merged subarray
k = 0
# Copy data to temp arrays L[] and R[]
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i = i + 1
else:
arr[k] = R[j]
j = j + 1
k = k + 1
# Checking if there're some remaining elements
while i < len(L):
arr[k] = L[i]
i = i + 1
k = k + 1
while j < len(R):
arr[k] = R[j]
j = j + 1
k = k + 1
# Function to print the elements
# of the array
def printArray(arr, size):
for i in range(size):
print(arr[i], end=" ")
print()
# Driver code
arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ]
size = len(arr)
print("Unsorted array:")
printArray(arr, size)
mergeSort(arr)
print("Sorted array:")
printArray(arr, size)
Выход:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19Понимание других алгоритмов сортировки
Сортировка – один из наиболее часто используемых алгоритмов программирования. Вы можете сортировать элементы на разных языках программирования, используя различные алгоритмы сортировки, такие как быстрая сортировка, пузырьковая сортировка, сортировка слиянием, сортировка вставкой и т. Д.
Пузырьковая сортировка – лучший выбор, если вы хотите узнать о простейшем алгоритме сортировки.