Как использовать сортировку по выделению

Сортировка по выбору – это метод сортировки, который выбирает элемент списка, а затем меняет его место другим. Он выбирает самый большой элемент, а затем меняет его местами на элемент с самым высоким индексом списка.

Алгоритм повторяет это несколько раз, пока список не будет отсортирован. Если вы не совсем уверены, как работает сортировка по выбору, вы попали в нужное место. Мы объясним это более подробно ниже и покажем вам пример.

Сортировка выбора: более пристальный взгляд

Предположим, у вас есть список: [39, 82, 2, 51, 30, 42, 7]. Чтобы отсортировать список с помощью сортировки по выбору, вам нужно сначала найти в нем наибольшее число.

В данном списке это число 82. Поменяйте местами 82 на число в наивысшем индексе (то есть 7).

После первого прохода новый порядок списка будет следующим: [39, 7, 2, 51, 30, 42, 82]. Каждый раз, когда алгоритм просматривает весь список, это называется «проход».

Обратите внимание, что список поддерживает отсортированный подсписок и несортированный подсписок во время процесса сортировки.

Связанный: Что такое нотация Big-O?

Исходный список начинается с отсортированного списка из нуля элементов и несортированного списка всех элементов. Затем после первого прохода у него есть отсортированный список, содержащий только номер 82.

На втором проходе самым большим числом в несортированном подсписке будет 51. Это число будет заменено на 42, чтобы задать новый порядок списка ниже:

[39, 7, 2, 42, 30, 51, 82].

Процесс повторяется до тех пор, пока не будет отсортирован весь список. На рисунке ниже представлен весь процесс:

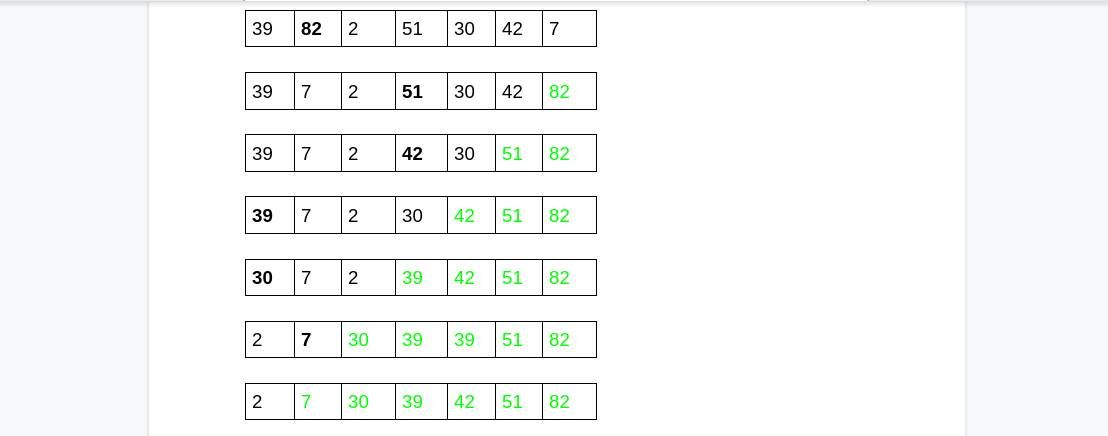
Цифры, выделенные жирным черным шрифтом, показывают самое высокое значение списка на тот момент. Зеленым цветом показан отсортированный подсписок.

Анализ алгоритмов

Чтобы понять сложность (с использованием нотации Big-O) этого алгоритма, выполните следующие действия:

На первом проходе выполняется (n-1) сравнений. На втором проходе (n-2). На третьем проходе (n-3) и так далее до (n-1) -го прохода, который выполняет только одно сравнение.

Обобщая приведенные ниже сравнения, получаем:

(П-1) + (П-1) + (П-1) + … + 1 = ((П-1) П) / 2.

Следовательно, сортировка выбора – O (n ² ).

Реализация кода

В коде показаны функции, которые можно использовать для выполнения сортировки выбора с использованием Python и Java.

Python:

 def selectionSort(mylist):
 for x in range(len(mylist) - 1, 0, -1):
 max_idx = 0
 for posn in range(1, x + 1):
 if mylist[posn] > mylist[max_idx]:
 max_idx = posn
 temp = mylist[x]
 mylist[x] = mylist[max_idx]
 mylist[max_idx] = temp

Джава:

 void selectionSort(int my_array[]){
 for (int x = 0; x < my_array.length - 1; x++)
 {
 int index = x;
 for (int y = x + 1; y < my_array.length; y++){
 if (my_array[y] < my_array[index]){
 index = y; // find lowest index
 }
 }
 int temp = my_array[index]; // temp is a temporary storage
 my_array[index] = my_array[x];
 my_array[x] = temp;
 }}

Переход от сортировки выбора к сортировке слиянием

Как показал приведенный выше анализ алгоритма, алгоритм сортировки выбора – O (n ² ). Он имеет экспоненциальную сложность и поэтому неэффективен для очень больших наборов данных.

Намного лучше использовать алгоритм сортировки слиянием со сложностью O (nlogn). И теперь вы знаете, как работает сортировка по выбору, следующей в вашем списке для изучения алгоритмов сортировки должна быть сортировка слиянием.