Руководство по бинарным деревьям для новичков
Если вы прошли курс по структурам данных в области информатики или являетесь программистом-самоучкой, скорее всего, вы встречали термин «двоичные деревья». Хотя они могут показаться немного сложными и сложными, концепция двоичного дерева довольно проста.
Читайте дальше, когда мы анализируем двоичные деревья и почему они являются необходимой базовой концепцией для программистов.
Что такое двоичные деревья?
Двоичные деревья являются одними из первых структур данных, которым студенты обучаются в курсе структур данных. Двоичное дерево состоит из множества узлов, и каждый узел двоичного дерева содержит два указателя, которые указывают левый и правый дочерние узлы данных.
Первый узел в двоичном дереве называется «корнем». Узлы последнего уровня в дереве называются листьями.
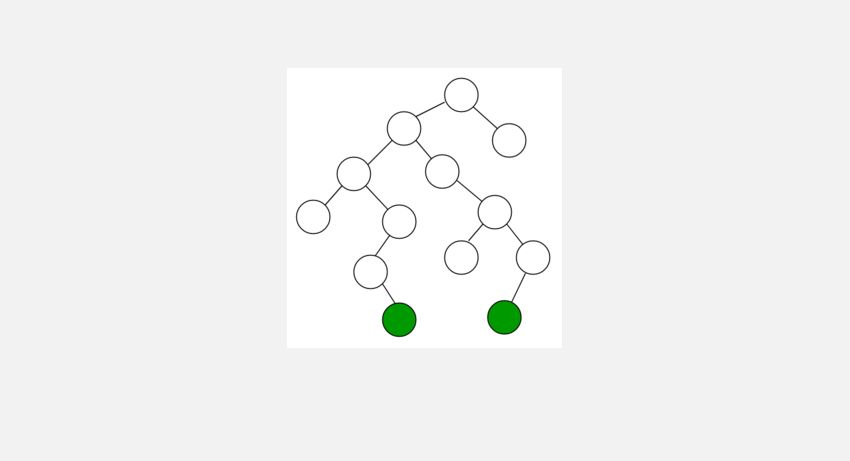
Каждый узел содержит элемент данных и два указателя узла. Пустое двоичное дерево представлено нулевым указателем. Как вы, возможно, уже догадались, двоичные деревья могут иметь только двух дочерних элементов (отсюда и название).
Типы бинарных древовидных структур
В зависимости от расположения узлов существует несколько различных структур двоичного дерева. Двоичное дерево называется полным двоичным деревом, если каждый узел в дереве имеет либо ноль, либо двух дочерних элементов. В идеальном двоичном дереве все узлы имеют двух дочерних элементов, и все листья имеют одинаковую глубину.
В полном двоичном дереве узлы заполнены на каждом уровне, за исключением последнего уровня. В полных бинарных деревьях узлы сосредоточены слева от корня. Другой распространенной структурой является сбалансированное двоичное дерево; в этой структуре высота правого и левого поддеревьев должна отличаться не более чем на единицу. Также требуется, чтобы левое и правое поддеревья также были сбалансированы.
Важно отметить, что высота сбалансированного двоичного дерева равна O (logn), где n – количество узлов в дереве.
В некоторых случаях, если у каждого узла есть только один левый или правый дочерний элемент, то двоичное дерево может стать искаженным двоичным деревом. Тогда он будет вести себя как связанный список, такие деревья также называются вырожденными деревьями.
Что такое деревья двоичного поиска?
Двоичное дерево поиска (BST) – это, по сути, упорядоченное двоичное дерево со специальным свойством, известным как свойство «двоичного дерева поиска». Свойство BST означает, что узлы со значением ключа меньше корня помещаются в левое поддерево, а узлы со значением ключа больше корня являются частью правого поддерева.
Свойство BST должно быть истинным для каждого последующего родительского узла в дереве.
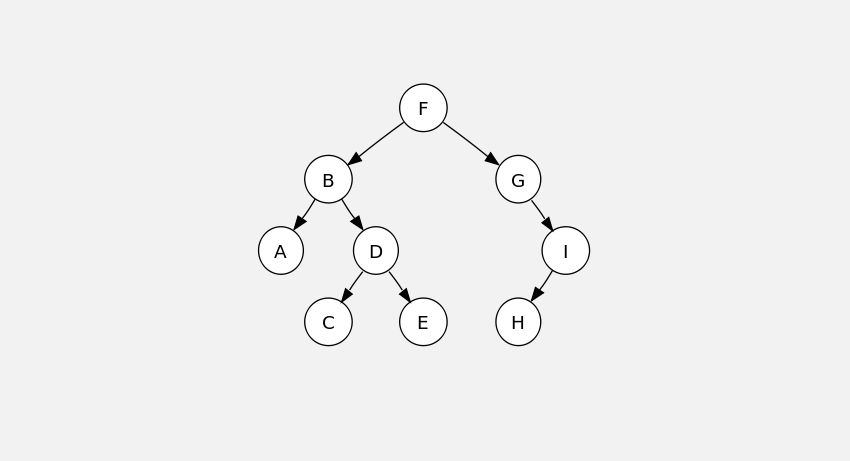
Деревья двоичного поиска предлагают быструю вставку и поиск. Операции вставки, удаления и поиска имеют временную сложность наихудшего случая O (n), что аналогично связному списку.
Преимущества двоичных деревьев
Двоичные деревья предлагают множество преимуществ, поэтому они остаются очень полезной структурой данных. Их можно использовать для отображения структурных отношений и иерархий в наборе данных. Что еще более важно, двоичные деревья обеспечивают эффективный поиск, удаление и вставку.
Также очень легко реализовать и поддерживать двоичное дерево. Бинарное дерево предлагает программистам преимущества упорядоченного массива и связанного списка; поиск в двоичном дереве выполняется так же быстро, как и в отсортированном массиве, а операции вставки или удаления столь же эффективны, как и в связанных списках.
Двоичные деревья – важные структуры данных
Двоичные деревья – это очень важная структура данных, и очень важно, чтобы программисты могли легко применять их в своих программах. Часто интервьюеры задают простые задачи двоичного дерева, такие как обход, максимальная глубина, зеркальное отображение и т. Д.
Мы настоятельно рекомендуем понять концепцию двоичного дерева и ознакомиться с типичными задачами собеседования.