Динамическое программирование: примеры, общие проблемы и решения
Нет сомнений в том, что проблемы динамического программирования могут быть очень пугающими на собеседовании по кодированию. Даже если вы знаете, что проблему необходимо решить с помощью метода динамического программирования, сложно найти рабочее решение в ограниченные сроки.
Лучший способ научиться решать задачи динамического программирования – решить как можно больше из них. Хотя вам не обязательно запоминать решение каждой проблемы, хорошо иметь представление о том, как его реализовать.
Что такое динамическое программирование?
Проще говоря, динамическое программирование – это метод оптимизации рекурсивных алгоритмов, большинство из которых используются для решения вычислительных или математических задач.
Вы также можете назвать это алгоритмическим методом решения проблемы оптимизации, разбив ее на более простые подзадачи. Ключевой принцип, на котором основано динамическое программирование, заключается в том, что оптимальное решение проблемы зависит от решений ее подзадач.
Везде, где мы видим рекурсивное решение, которое повторяет вызовы одних и тех же входных данных, мы можем оптимизировать его с помощью динамического программирования. Идея состоит в том, чтобы просто сохранить результаты подзадач, чтобы нам не приходилось повторно вычислять их, когда это понадобится позже.
Динамически запрограммированные решения имеют полиномиальную сложность, которая обеспечивает гораздо более быстрое выполнение, чем другие методы, такие как рекурсия или обратный поиск. В большинстве случаев динамическое программирование сокращает временную сложность, также известную как big-O , от экспоненциальной до полиномиальной.
Теперь, когда у вас есть хорошее представление о том, что такое динамическое программирование, пришло время проверить несколько распространенных проблем и их решения.
Проблемы динамического программирования
1. Задача о рюкзаке
Постановка задачи
Учитывая набор элементов, каждый из которых имеет вес и значение, определите количество каждого элемента для включения в коллекцию, чтобы общий вес не превышал заданный предел, а общее значение было как можно большим.
Вам даны два целочисленных массива значений [0..n-1] и веса [0..n-1], которые представляют значения и веса, связанные с n элементами соответственно. Также дано целое число W, которое представляет вместимость ранца.
Здесь мы решаем задачу о ранце 0/1, а это значит, что мы можем либо добавить предмет, либо исключить его.
Алгоритм
- Создайте двумерный массив с n + 1 строкой и w + 1 столбцом. Номер строки n обозначает набор предметов от 1 до i , а номер столбца w обозначает максимальную грузоподъемность сумки.
- Числовое значение в [i] [j] обозначает общую стоимость предметов до i в сумке, которая может нести максимальный вес j.
- Для каждой координаты [i] [j] в массиве выберите максимальное значение, которое мы можем получить без элемента i , или максимальное значение, которое мы можем получить с элементом i, в зависимости от того, что больше.
- Максимальное значение, которое можно получить, включив элемент i, представляет собой сумму самого элемента i и максимальное значение, которое может быть получено с оставшейся вместимостью ранца.
- Выполняйте этот шаг, пока не найдете максимальное значение для W- й строки.
Код
def FindMax(W, n, values, weights):
MaxVals = [[0 for x in range(W + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
MaxVals[i][w] = 0
elif weights[i-1] <= w:
MaxVals[i][w] = max(values[i-1]
+ MaxVals[i-1][w-weights[i-1]],
MaxVals[i-1][w])
else:
MaxVals[i][w] = MaxVals[i-1][w]
return MaxVals[n][W]
2. Проблема со сменой монеты
Постановка задачи
Предположим, вам дан массив чисел, представляющих стоимость каждой монеты. Учитывая определенную сумму, найдите минимальное количество монет, необходимых для ее получения.

Алгоритм
- Инициализируйте массив размером n + 1 , где n – количество. Инициализируйте значение каждого индекса i в массиве, равное его сумме. Это означает максимальное количество монет (с использованием монет достоинством 1), необходимое для создания этой суммы.
- Поскольку для 0 нет обозначения, инициализируйте базовый случай, когда array [0] = 0 .
- Для каждого другого индекса i мы сравниваем значение в нем (которое изначально установлено на n + 1 ) с массивом значений [ik] +1 , где k меньше i . По сути, это проверяет весь массив до i-1, чтобы найти минимально возможное количество монет, которое мы можем использовать.
- Если значение в любом массиве [ik] + 1 меньше, чем существующее значение в массиве [i] , замените значение в массиве [i] значением в массиве [ik] +1 .
Код
def coin_change(d, amount, k):
numbers = [0]*(amount+1)
for j in range(1, amount+1):
minimum = amount
for i in range(1, k+1):
if(j >= d[i]):
minimum = min(minimum, 1 + numbers[jd[i]])
numbers[j] = minimum
return numbers[amount]
3. Фибоначчи
Постановка задачи
Ряд Фибоначчи – это последовательность целых чисел, где следующее целое число в ряду является суммой двух предыдущих.
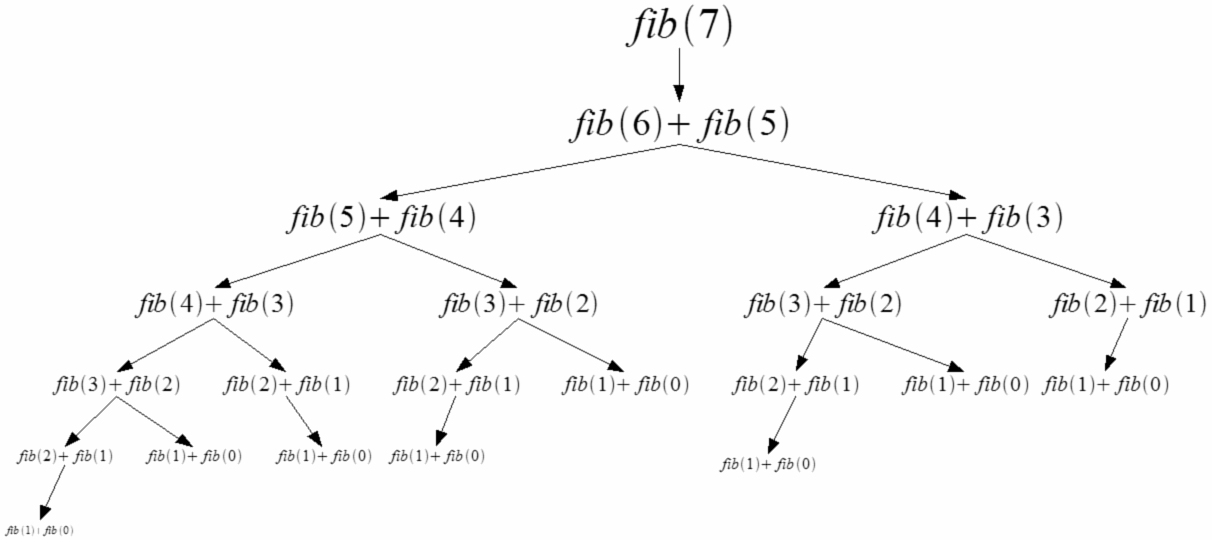
Он определяется следующим рекурсивным соотношением: F (0) = 0, F (n) = F (n-1) + F (n-2) , где F (n) – n- й член. В этой задаче мы должны сгенерировать все числа в последовательности Фибоначчи до заданного n- го члена.
Алгоритм
- Во-первых, используйте рекурсивный подход для реализации данного рекуррентного отношения.
- Рекурсивное решение этой проблемы влечет за собой разбиение F (n) на F (n-1) + F (n-2) , а затем вызов функции с F (n-1) и F (n + 2) в качестве параметров. Мы делаем это до тех пор, пока не будут достигнуты базовые случаи, когда n = 0 или n = 1 .
- Теперь мы используем метод, называемый мемоизацией. Сохраните результаты всех вызовов функций в массиве. Это гарантирует, что для каждого n F (n) нужно будет вычислить только один раз.
- Для любых последующих вычислений его значение можно просто получить из массива за постоянное время.
Код
def fibonacci(n):
fibNums = [0, 1]
for i in range(2, n+1):
fibNums.append(fibNums[i-1] + fibNums[i-2])
return fibNums[n]4. Самая длинная возрастающая подпоследовательность
Постановка задачи
Найдите длину самой длинной возрастающей подпоследовательности внутри данного массива. Самая длинная возрастающая подпоследовательность – это подпоследовательность в массиве чисел с возрастающим порядком. Числа в подпоследовательности должны быть уникальными и располагаться в порядке возрастания.
Кроме того, элементы последовательности не обязательно должны быть последовательными.
Алгоритм
- Начните с рекурсивного подхода, при котором вы вычисляете значение самой длинной возрастающей подпоследовательности каждого возможного подмассива от нулевого индекса до индекса i, где i меньше или равно размеру массива.
- Чтобы превратить этот метод в динамический, создайте массив для хранения значений для каждой подпоследовательности. Инициализируйте все значения этого массива равными 0.
- Каждый индекс i этого массива соответствует длине самой длинной возрастающей подпоследовательности для подмассива размера i .
- Теперь при каждом рекурсивном вызове findLIS (arr, n) проверяйте n- й индекс массива. Если это значение равно 0, то вычислите значение, используя метод на первом шаге, и сохраните его в n- м индексе.
- Наконец, верните максимальное значение из массива. Это длина самой длинной возрастающей подпоследовательности заданного размера n .
Код
def findLIS(myArray):
n = len(myArray)
lis = [0]*n
for i in range (1 , n):
for j in range(0 , i):
if myArray[i] > myArray[j] and lis[i]< lis[j] + 1 :
lis[i] = lis[j]+1
maxVal= 0
for i in range(n):
maxVal = max(maxVal , lis[i])
return maxValРешения задач динамического программирования
Теперь, когда вы рассмотрели некоторые из самых популярных проблем динамического программирования, пришло время попробовать реализовать решения самостоятельно. Если вы застряли, вы всегда можете вернуться и обратиться к разделу алгоритмов для каждой проблемы выше.
Учитывая, насколько популярны сегодня такие методы, как рекурсия и динамическое программирование, не помешает проверить некоторые популярные платформы, на которых вы можете изучить такие концепции и отточить свои навыки программирования . Хотя вы можете не сталкиваться с этими проблемами ежедневно, вы наверняка столкнетесь с ними на техническом собеседовании.
Естественно, знание общих проблем обязательно принесет дивиденды, когда вы пойдете на следующее собеседование. Итак, откройте свою любимую IDE и приступайте к работе!